Next Token Generation Strategy
April 19, 2025
Auto-regressive language generation is based on the assumption that the probability distribution of a word sequence $w_{1:T}$ can be decomposed into the product of conditional next word distributions:
\[P(w_{1:T} \mid W_0) = \prod^{T}\_{t=1} P(w_t \mid w_{1:t-1}, W_0)\]where one word prediction $w_t$ is conditioned on all previous word choices $w_{1:t-1}$ and an initial context word sequence $W_0$.
The currently most prominent decoding methods are Greedy search, Beam search, and Sampling.
Greedy Search
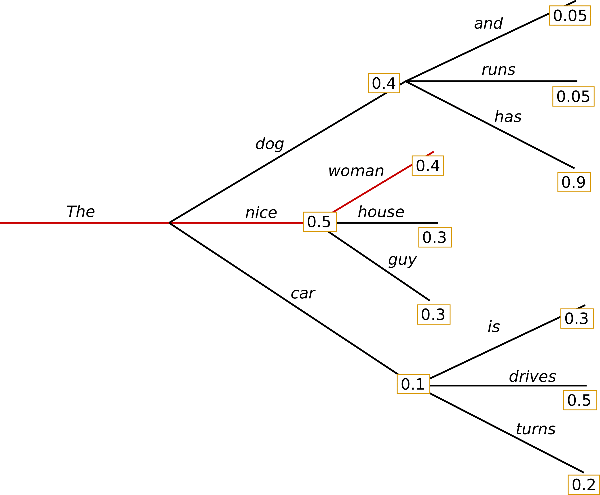
Greedy search simply selects next word $w_t$ with the highest probability given this branch layer probability distribution $W_t$ that is chosen from previous word choices $w_{t-1}$, such that $w_t=\argmax_{w}P(w\mid w_{1:t-1})$.
For example, starting from ${ \text{The} }$ with $W_0={ 1 }$, given ${ \text{dog}, \text{nice}, \text{car} }$ corresponding probability distribution $W_1 = { 0.4, 0.5, 0.1 }$, select “nice”; then based on chosen “nice”’s next word probability distribution, select “woman”.
</br>
By default, it is the generate(...)’s implementation in huggingface.
greedy_output = model.generate(**model_inputs, max_new_tokens=40)
Beam Search
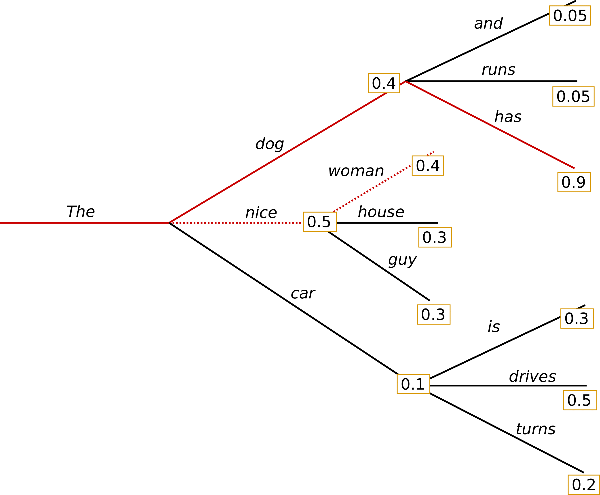
However, some words may have very high probabilities but hidden from previous words that have low probabilities, but the total chained probability is higher than a greedy search’s result.
$0.36 = 1 \times 0.4 \times 0.9$ by the choice ${ \text{The}, \text{dog}, \text{has} }$ is the final choice for it is higher than $0.2 = 1 \times 0.5 \times 0.4$ by the choice ${ \text{The}, \text{nice}, \text{woman} }$.
The next beam search is another greedy search but from the probability distribution without the previous greedy search results. For example, in the figure below, the second greedy search draws from word candidates ${ \text{dog}, \text{car} }$ for “nice” is already chosen by the previous greedy search.
</br>
num_beams is an argument to pass into generate(...) to enable the beam search method.
# activate beam search and early_stopping
beam_output = model.generate(**model_inputs, max_new_tokens=40,
num_beams=5, early_stopping=True)
Constrained Beam Search
If there is prior that certain words, or concatenation of certain tokens such as play and ##ing must/should be highly likely present, manual updated probability distribution can be constructed to cater this need.
Multiple Beams vs Single Beam (Greedy Search)
For similar inputs with identical semantics, multi-beam search has stable results compared to just one greedy search.
dataInputSentence = []
dataInputSentence.append("Hand me a recipe of making bolognese pasta:")
dataInputSentence.append("Give a recipe of how to make bolognese pasta:")
dataInputSentence.append("Give me a recipe of preparing bolognese pasta:")
dataInput = tokenizer(dataInputSentence, return_tensors="pt",
truncation=True, padding=True).to(device)
preds_gens = model.generate(**dataInput)
print(tokenizer.decode(preds_gens[0], skip_special_tokens=True))
print(tokenizer.decode(preds_gens[1], skip_special_tokens=True))
print(tokenizer.decode(preds_gens[2], skip_special_tokens=True))
#### print the below
# Using a sprinkling of sprinkling of sp
# To make bolognese pasta, you can use a bolognese
# Using a frying pan, heat the pasta in a skillet over medium heat.
preds_gens = model.generate(**dataInput, num_beams=10)
print(tokenizer.decode(preds_gens[0], skip_special_tokens=True))
print(tokenizer.decode(preds_gens[1], skip_special_tokens=True))
print(tokenizer.decode(preds_gens[2], skip_special_tokens=True))
#### print the below
# Preheat oven to 350 degrees Fahrenheit (180 degrees Celsius) and line a baking
# Preheat oven to 350 degrees Fahrenheit (180 degrees Celsius) and line a baking
# Preheat oven to 350 degrees Fahrenheit (180 degrees Celsius). Preheat oven to 350
Sampling
Sampling simply means randomly selecting a word $w_t$ from the current branch layer $W_t$ disregarding their probability.
temperature controls randomness of selecting words, and $\text{temperature} \rightarrow 0$ gives the exact results as that of one greedy search.
sample_output = model.generate(**model_inputs, max_new_tokens=40,
do_sample=True, top_k=0, temperature=0.6)
Top-K Sampling
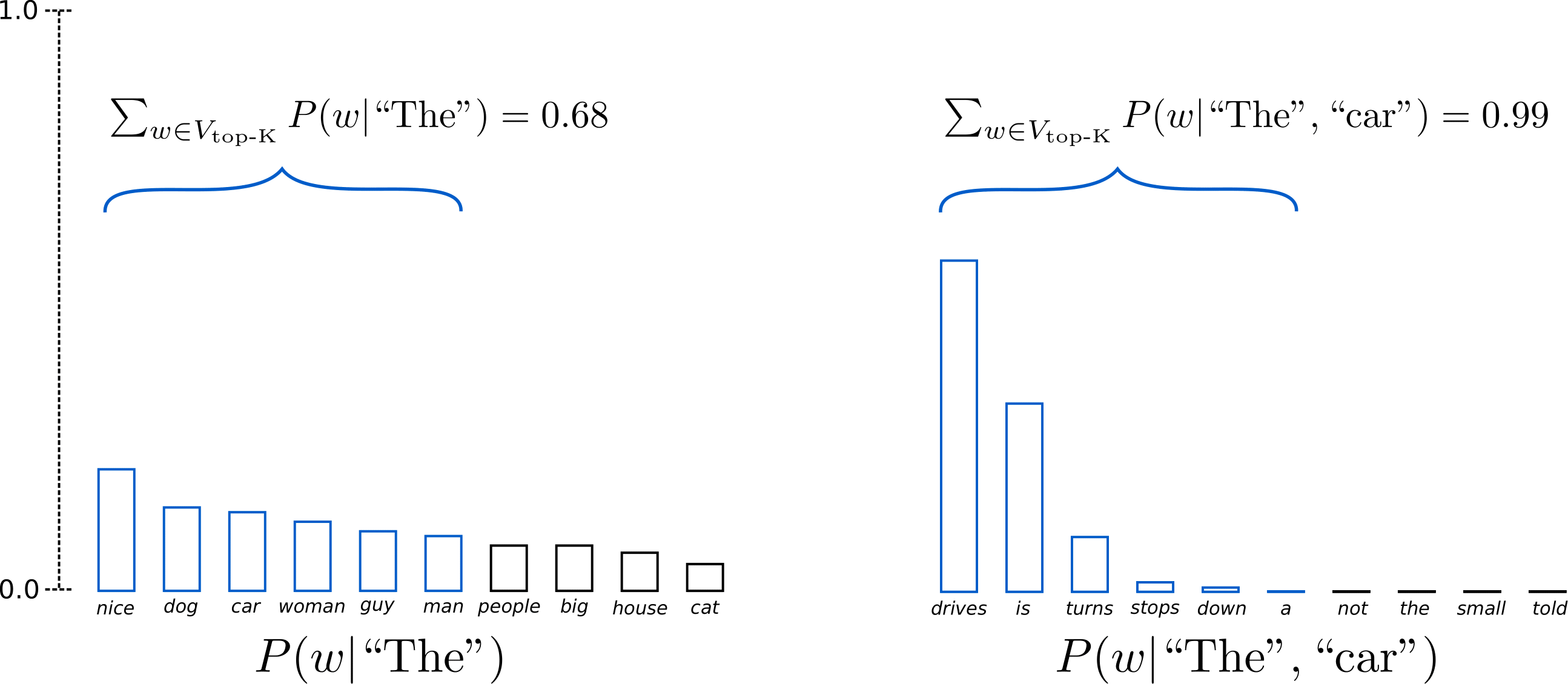
At the step $t$, randomly select the word $w_t$ only from the top $K$ word set $V_{\text{top-K}_t}$ by their probabilities. As a result, the distribution is very small that reduces unnecessary checks on low probability tokens.
</br>
The above figure shows that, given randomly selected word $w_1=\text{car}$ from the first $K=6$ candidates, the next 6 candidate words from the “car”’s branch are ${ \text{drives}, \text{is}, \text{turns}, \text{stops}, \text{down}, \text{a} }$, and by probability, the 6 words are $99\%$ likely being chosen such that $\sum_{w\in V_{\text{top-K}}}P(w_2\mid\text{The}, \text{car})=0.99$.
This is for in NLP, the first few tokens contain rich info guiding what aspect a sentence is describing (prefix-tuning borrows this idea), so that the remaining sequence tokens are almost certain.
# set top_k to 50
sample_output = model.generate(**model_inputs, max_new_tokens=40,
do_sample=True, top_k=50)
Top-P Sampling
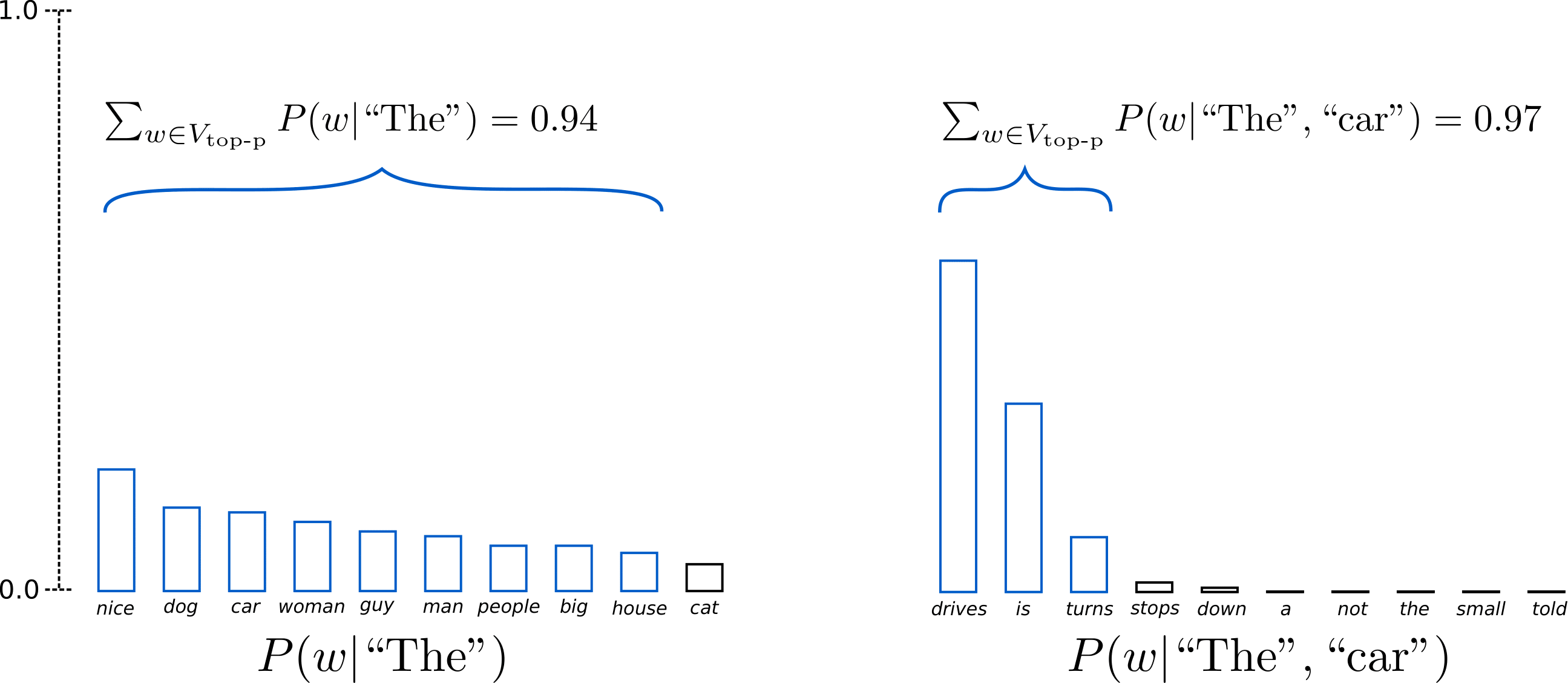
Similar to Top-K sampling, but the threshold is set to top tokens’ accumulated probability, that only top probability tokens whose accumulated probability slightly greater than the threshold are selected.
For example, set a threshold of $0.92$, assume probability of “house” is $0.03$, and assume $V_{\text{top-P}_{1, K=8}}={ \text{nice}, \text{dog}, \text{car}, \text{woman}, \text{guy}, \text{man}, \text{people}, \text{big} }$, and $\sum_{w\in V_{\text{top-P}_{1, K=8}}}P(w_1\mid\text{The})=0.91<0.92$. Hence, should consider next token to see if the accumulated probability exceeds the threshold of $0.92$. Having included the new token “house” $V_{\text{top-P}_{1, K=9}}={ V_{\text{top-P}_{1, K=8}}, \text{house} }$, the new accumulated probability is $\sum_{w\in V_{\text{top-P}_{1, K=9}}}P(w_1\mid\text{The})=0.94>0.92$, hence only the top 9 words are picked.
</br>
# set top_p to 0.92
sample_output = model.generate(**model_inputs, max_new_tokens=40,
do_sample=True, top_k=0, top_p=0.92)