U-Net

September 07, 2025

U-Net

U-Net was originally designed to do image segmentation with small training dataset, then adopted in other vision tasks for its great capability in contextual information comprehension and precise localization.

The down-sampling then up-sampling shape gives the network name “U”.

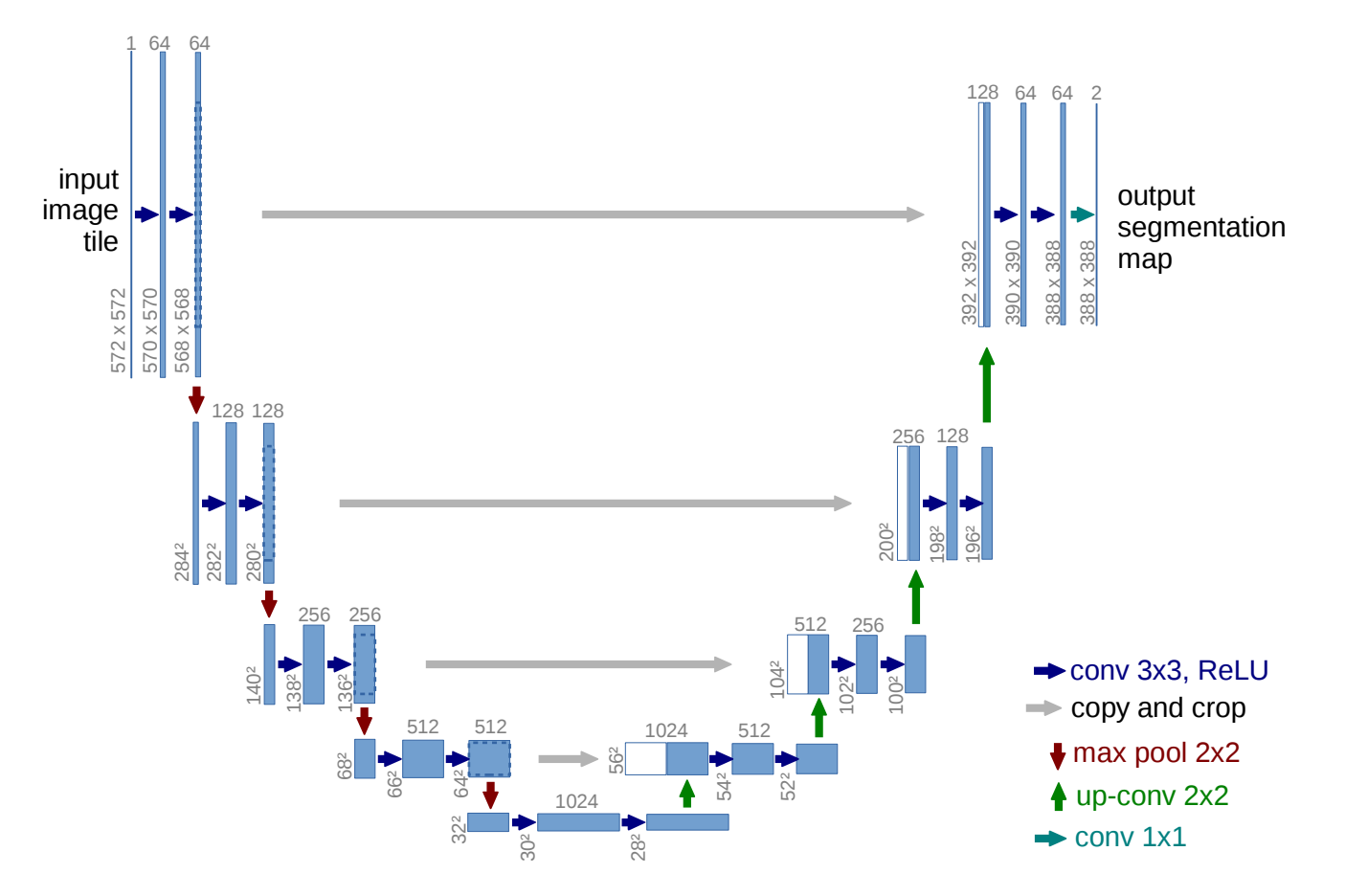
</br>

Architecture:

• The Contracting Path (Encoder) for down-sampling: This part of the network follows a typical CNN architecture.
• The Expansive Path (Decoder): The decoder’s role is to upsample the feature maps back to the original image resolution while preserving the learned feature information.
• Skip Connections: These connections link the output of the convolutional layers in the contracting path to the input of the corresponding layers in the expansive path.

The process of skipping + decoder:

1. Get input from encoder at the same layer $X_{enc}^{[l]}\in\mathbb{R}^{2H\times 2W\times C}$
2. Get input from a deeper layer $X_{dec}^{[l+1]}\in\mathbb{R}^{H\times W\times C}$
3. Up-sample $X_{dec}^{[l+1]}$ to $X_{up}^{[l]}\in\mathbb{R}^{2H\times 2W\times C}$
4. Concatenate the two inputs $X_{concat}^{[l]}=[X_{up}^{[l]};X_{enc}^{[l]}]\in\mathbb{R}^{2H\times 2W\times 2C}$
5. Apply kernel $K\in\mathbb{R}^{k\times k}$ (e.g., $k=3$) to $X_{concat}^{[l]}$ by up-convolution and get the output $X_o^{[l]}\in\mathbb{R}^{2H\times 2W\times C}$

The innovative approach is that

• The concatenation $X_{concat}^{[l]}=[X_{up}^{[l]};X_{enc}^{[l]}]$ mathematically presents the network with both streams of information simultaneously. For every pixel location, the subsequent convolutional filters have access to both the “what” (from X_upsampled’s channels) and the “where” (from X_down’s channels).
• The up-convolution learns the optimal way to merge these streams.

Additive Attention U-Net

The novel additive attention is illustrated in this academic “Attention U-Net: Learning Where to Look for the Pancreas”

Reference: https://smcdonagh.github.io/papers/attention_u_net_learning_where_to_look_for_the_pancreas.pdf

In contrast to the typical dot-product attention, it uses “signal” and “gate”.

The attention gate takes the encoder feature map $X_{enc}^{[l]}$ and the up-sampled decoder feature map (gating signal) $X_{up}^{[l]}$ as inputs to compute an attention map $\mathbf{a}^{[l]}$.

Denote feature map $X_{enc}^{[l]}$ as $\mathbf{x}$, up-sampled signal $X_{up}^{[l]}$ as gate $\mathbf{g}$.

Linear Weight

\[\theta(\mathbf{x}) = W_{x}^{\top} \mathbf{x} + \mathbf{b}_x \in \mathbb{R}^{2H\times 2W\times C_{in}}\] \[\phi(\mathbf{g}) = W_{g}^{\top} \mathbf{g} + \mathbf{b}_g \in \mathbb{R}^{2H\times 2W\times C_{in}}\]

Additive (Bahdanau-style) Attention

Different from transformer (scaled dot-product attention $QK^{\top}$), additive attention $\text{ReLU}\big(\theta(x) + \phi(g)\big)$ combines the two input tensors (input signals and gates) and uses a learned weight vector ($W_s^{\top}$) to decide on the importance of each spatial location.

\[\mathbf{s}^{[l]} = \text{ReLU}(\theta(\mathbf{x}) + \phi(\mathbf{g})) \in \mathbb{R}^{2H\times 2W\times C_{in}} \\ \mathbf{a}^{[l]} = \sigma(W_s^{\top} \mathbf{s}^{[l]} + \mathbf{b}_s) \in \mathbb{R}^{2H\times 2W\times 1}\]

where $\sigma(.)$ is the sigmoid function. The resulting ($\mathbf{a}^{[l]}$) is a spatial map where values close to $1$ indicate regions of high relevance.

Denote $\odot$ as an element-wise operation. $\hat{X}_{enc}^{[l]}$ is attention-filtered encoder input.

\[\hat{X}_{enc}^{[l]} = X_{enc}^{[l]} \odot \mathbf{a}^{[l]} \in \mathbb{R}^{2H\times 2W\times C_{enc}}\]

Finally, $\hat{X}{enc}^{[l]}$ and $X{up}^{[l]}$ are concatenated and applied convolution $K\in\mathbb{R}^{k\times k\times(C_{enc}+C_{dec})}$ to derive $X_o^{[l]}\in\mathbb{R}^{2H\times 2W\times C_{o}}$.

\[\begin{align*} X_{concat}^{[l]} &=[\hat{X}_{enc}^{[l]};X_{up}^{[l]}]\in\mathbb{R}^{2H\times 2W\times (C_{enc}+C_{dec})} \\ K \otimes X_{concat}^{[l]} &= X_o^{[l]}\in\mathbb{R}^{2H\times 2W\times C_{o}} \end{align*}\]

Cross-Attention with CLIP Embeddings for U-Net

This mechanism is typically used for text-to-image generation.

Contrastive Language-Image Pre-training (CLIP)

Contrastive Language-Image Pre-training, or CLIP, is a neural network developed by OpenAI designed to understand the relationship between images and text, e.g., vision feature as embeddings vs text token embeddings.

CLIP learns from a massive dataset of 400 million image-text pairs scraped from the internet.

</br>

To achieve this shared understanding, CLIP employs a dual-encoder architecture:

• Image Encoder: This component, typically a Vision Transformer (ViT) or a ResNet, processes an image and outputs a high-dimensional vector, or “embedding,” that encapsulates the visual information of the image.
• Text Encoder: A Transformer-based model processes a textual description and produces a corresponding embedding in the same dimensional space as the image embeddings.

For training:

define a batch of $N$ image-text pairs, let $\mathbf{v}_i$ be the embedding for the $i$-th image and $\mathbf{u}_i$ be the embedding for its corresponding text description. The loss function is defined as:

\[L = - \frac{1}{N} \sum_{i=1}^{N} \left[ \log\frac{\exp(\mathbf{v}_i \cdot \mathbf{u}_i / \tau)}{\sum_{j=1}^{N} \exp(\mathbf{v}_i \cdot \mathbf{w}_j / \tau)} \right] - \frac{1}{N} \sum_{i=1}^{N} \left[ \log\frac{\exp(\mathbf{v}_i \cdot \mathbf{u}_i / \tau)}{\sum_{j=1}^{N} \exp(\mathbf{v}_j \cdot \mathbf{u}_i / \tau)} \right]\]

where

• $\mathbf{v}_i \cdot \mathbf{u}_i$ is the dot product between the embedding of the i-th image and the j-th text description, representing their cosine similarity.
• $\tau$ is a learnable temperature parameter that scales the similarity scores.

Cross-Attention Module Insertion

Instead of directly concatenating $X_{concat}^{[l]}=[X_{up}^{[l]};X_{enc}^{[l]}]$, first modify $X_{up}^{[l]}$ using the text embeddings $E\in\mathbb{R}^{L\times D}$, where $L$ is the length of prompt/tokens, $D$ is the embedding dimension.

In the context of text-to-image generation, the image features will form the Query, and the text embeddings will form the Key and Value.

• Query (Q): Derived from the image features. It asks, “For each pixel, what parts of the text are relevant?”

\[Q = X_{up} W_Q \in \mathbb{R}^{(2H \cdot 2W) \times d_k}\]

• Key (K): Derived from the text embeddings. It represents the semantic content of the text that can be “looked up.”

\[K = E W_K \in \mathbb{R}^{L \times d_k}\]

• Value (V): Also derived from the text embeddings. It represents the actual content that will be infused into the image features.

\[V = E W_V \in \mathbb{R}^{L \times d_v}\]

Apply the dot-product attention

\[\begin{align*} \text{AttentionWeights} &=\text{softmax}\left(\frac{QK^{\top}}{\sqrt{d_k}}\right) \in \mathbb{R}^{2W \times 2H \times L} \\ \text{Attention} &=\text{AttentionWeights}\space\cdot\space V \in \mathbb{R}^{2W \times 2H \times d_v} \end{align*}\]

For $Q = X_{up} W_Q$ that the $\text{Attention}$ shows from what up-sampled features are correlated to what text description from the pre-learned CLIP.

Then, the attention is projected back to the original spatial form

\[\text{Attention}_{proj} =\text{Attention}\space\cdot\space W_A \in \mathbb{R}^{2W \times 2H \times C_{dec}}\]

The projection by $W_A$ makes the text-image feature attentions map to spatial locations.

The projected attentions are added back to the original up-sampled $X_{up}^{[l]}$.

\[X_{att}^{[l]}=X_{up}^{[l]}+\text{Attention}_{proj} \in \mathbb{R}^{2W \times 2H \times C_{dec}}\]

Finally, $\hat{X}{enc}^{[l]}$ and $X{att}^{[l]}$ are concatenated and applied convolution $K\in\mathbb{R}^{k\times k\times(C_{enc}+C_{dec})}$ to derive $X_o^{[l]}\in\mathbb{R}^{2H\times 2W\times C_{o}}$.

\[\begin{align*} X_{concat}^{[l]} &=[\hat{X}_{enc}^{[l]};X_{att}^{[l]}]\in\mathbb{R}^{2H\times 2W\times (C_{enc}+C_{dec})} \\ K \otimes X_{concat}^{[l]} &= X_o^{[l]}\in\mathbb{R}^{2H\times 2W\times C_{o}} \end{align*}\]